
Κατασκευών
2.7. Ο συντελεστής Κ και ο Υπολογισμός των Τάσεων |
||||||
|
Ο ΣΥΝΤΕΛΕΣΤΗΣ ΕΝΤΑΣΗΣ ΤΑΣΕΩΝ Κ | |||||
Από τη προηγούμενη παράγραφο φαίνεται καθαρά πόσο σημαντικός είναι ο ρόλος του Συντελεστή Έντασης Τάσεων Κ, στη Θραυστομηχανική. Ο συντελεστής Κ μας χρειάζεται, είτε, για να υπολογίσουμε τη στατική αντοχή μιας κατασκευής με ρωγμή, είτε, την επέκταση μιας ρωγμής σε κατασκευή που φορτίζεται δυναμικά, είτε, την επέκταση μιας ρωγμής λόγω διάβρωσης σε μια φορτισμένη κατασκευή. Για να προβλέψουμε τη συμπεριφορά των ατελειών στα διάφορα υλικά, θα πρέπει να γνωρίζουμε ή να προσδιορίσουμε τη τιμή του συντελεστή Κ που αντιστοιχεί στη κάθε περίπτωση. Διακρίνουμε τρεις μορφές του συντελεστή Κ, μια για κάθε έναν από τους τρεις τρόπους (modes) φόρτισης μιας ρωγμής:
Οι τρεις τρόποι φόρτισης μιας ρωγμής (Ι, ΙΙ & ΙΙΙ) φαίνονται στην επόμενη εικόνα.
Ο Τρόπος Ι (εφελκυστική φόρτιση) συναντάται στη πλειοψηφία των περιπτώσεων και γι’ αυτό έχει λάβει πολύ μεγαλύτερη προσοχή σε θεωρητικό και πειραματικό επίπεδο. Ο Τρόπος ΙΙ (ολίσθηση) είναι ο λιγότερο συχνός και λιγότερο σημαντικός. Εμφανίζεται συνήθως μαζί με τον Ι ή ΙΙΙ οι ποίοι είναι και οι κυρίαρχοι τρόποι φόρτισης. Ο Τρόπος ΙΙΙ (ψαλιδισμός) εμφανίζεται κατά την στρέψη μιας ράβδου που φέρει ρωγμή.
Υπολογισμός των Τάσεων Έστω μια άπειρη πλάκα με μια κεντρική ρωγμή μήκους 2α η οποία φορτίζεται στο επίπεδο Χ-Υ με τάση σ.
Εφαρμόζοντας τις εξισώσεις ισορροπίας τάσεων και χρησιμοποιώντας τις συναρτήσεις Airy, τη λύση Westergaard, μιγαδικές μεταβλητές, τις εξισώσεις Cauchy-Riemann, οριακές συνθήκες και πολικές συντεταγμένες, τελικά (…) προκύπτει ότι, για κάθε ένα σημείο (r,θ) γύρω από το χείλος της ρωγμής (με r << α), οι τάσεις που αναπτύσσονται δίνονται από τους παρακάτω τύπους, που είναι της μορφής της εξίσωσης (12) που έδωσε ο Irwin:
Οι εξισώσεις αυτές μας δείχνουν ότι όλες οι τάσεις θα τείνουν στο άπειρο (σy → ∞) καθώς η απόσταση από το χείλος της ρωγμής θα τείνει στο μηδέν (r → 0). Βέβαια στη πράξη αυτό δεν συμβαίνει, γιατί η πραγματικότητα είναι πολύ πιο πολύπλοκη ώστε να περιγραφεί με τα απλοϊκά μοντέλα που χρησιμοποιούμε. Παρ’ όλα αυτά οι παραπάνω σχέσεις οδηγούν σε πολύ χρήσιμα πρακτικά αποτελέσματα. Παρατηρούμε ότι οι πιο πάνω εξισώσεις (16) έχουν ένα μέρος που εξαρτάται από τη θέση (r,θ) του σημείου (οι τριγωνομετρικοί όροι και ο παρονομαστής), και, έναν όρο (τον αριθμητή) ο οποίος εξαρτάται από τις υπόλοιπες παραμέτρους ή συνθήκες (φορτίο, μήκος ρωγμής, γεωμετρία, κλπ.) Ο όρος αυτός δεν είναι άλλος από τον συντελεστή έντασης τάσεων για τη περίπτωση της άπειρης πλάκας ( Χρησιμοποιώντας αντίστοιχα τους συντελεστές ΚΙ, ΚΙΙ, & ΚΙΙΙ, για κάθε ένα τρόπο φόρτισης (Ι, ΙΙ & ΙΙΙ), οι εξισώσεις των τάσεων που προκύπτουν είναι:
Υπολογισμός του Συντελεστή ΚΙ Η πλειοψηφία των περιπτώσεων που έχουν μελετηθεί πειραματικά και θεωρητικά αφορούν τον τρόπο φόρτισης Ι (άνοιγμα ή εφελκυσμός) και τον συντελεστή ΚΙ, και με αυτές τις περιπτώσεις θα ασχοληθούμε. Η πλέον γνωστή και απλή μορφή του συντελεστή Κ είναι αυτή της εξίσωσης Η σχέση αυτή ισχύει για την ιδανική περίπτωση μιας άπειρης πλάκας και η πραγματικότητα σχεδόν πάντα διαφέρει. Η γενική μορφή του ΚΙ είναι:
Όπως είδαμε πιο πάνω, για την άπειρη πλάκα ή την πλάκα μεγάλου πλάτους w με κεντρική ρωγμή 2α (2α << w), ο ΚΙ είναι:
Η τιμή της παράστασης f(.) διαφέρει ανάλογα με τη γεωμετρία του δοκιμίου. Για την άπειρη πλάκα είναι μονάδα (f = 1). Οι τιμές της ποσότητας f(α/w) για διάφορες περιπτώσεις δοκιμίων περιέχονται στον παρακάτω πίνακα:
Αντοχή Θραύσης ΚΙC ή ΚC Ο συντελεστής ΚΙ αυξάνει με την αύξηση της τάσης φόρτισης σ. Όταν η τιμή του ξεπεράσει μια κρίσιμη τιμή ΚΙC τότε η ρωγμή επεκτείνεται. Η κρίσιμη αυτή τιμή του συντελεστή ονομάζεται Αντοχή Θραύσης ή Σκληρότητα Θραύσης. Με βάση την εξίσωση (15) και έχοντας βρει πειραματικά τις τιμές του συντελεστή KC για ένα υλικό, μπορούμε να σχεδιάσουμε τη καμπύλη και να υπολογίζουμε για κάθε φορτίο ποιο είναι το επιτρεπόμενο μήκος ρωγμής ή για μια δεδομένη ρωγμή ποιο είναι το επιτρεπόμενο φορτίο. Στο επόμενο διάγραμμα φαίνεται πως χρησιμοποιούμε την καμπύλη του KC για να υπολογίσουμε τις επιτρεπόμενες τάσεις ή ρωγμές.
Παράδειγμα: Για τη τάση σχεδίασης των 138 MPa το επιτρεπόμενο μήκος ρωγμής είναι 145 mm, ενώ για τα 310 MPa το επιτρεπόμενο μήκος ρωγμής είναι μόνο 27.9 mm. Αλλάζοντας υλικό με μεγαλύτερο KC (από steel1 σε steel2) βλέπουμε ότι θα αυξηθούν και οι ανοχές της κατασκευής μας. Πίνακας: Τιμές των συντελεστών KIC & GC για διάφορα υλικά
|
||||||
 K(Ι,ΙΙ,ΙΙΙ)
K(Ι,ΙΙ,ΙΙΙ) 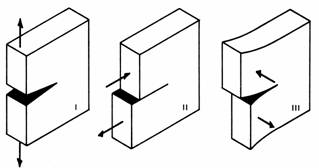


 ,
,  ,
,  (16)
(16) (17)
(17) (18)
(18) (19)
(19) (20)
(20) (21)
(21)
